المناهج المدرسيَّة والهندسة الكسوريَّة
أديب الخوري
شبه مقدِّمة
أودُّ بدايةً أن أنوِّه إلى أنَّ هذا البحث يندرج ضمن سياق بحوثٍ أخرى
ويشكِّل متابعةً لمحاولة أو مجموعة محاولات لتقديم منظور جديد إلى
المناهج المدرسيَّة أو ما يمكن أن تكون عليه في المستقبل هذه المناهج.
ولا بدَّ لي أن أؤكِّد في المناسبة أنَّني أتناول الموضوع من منظور
عامٍّ أي أوسع من محلِّيِّ وأبعد من آنيِّ.
سبق أن قدَّمتُ على نحو خاصٍّ في الجمعيَّة الكونيَّة السُّوريَّة
محاضرَتين تصبَّان في نفس المجرى: أساليب تعليم الرِّياضيَّات
(2011) والمناهج المدرسيَّة وعلوم الفضاء (2013)[1].
تأتي محاضرة اليوم حلقةً في سلسلةٍ يمكن أن تمتدَّ أكثر، وهي لا تحاول
على الإطلاق أن تكون مقاربةً تفرض نفسها، بقدر ما أحاول من خلالها طرح
أفكار على بساط النِّقاش والمداولة تطلُّعًا إلى الوصول لما هو أفضل.
ولكي أضع الحاضرين في الإطار العامِّ أذكِّر بأنَّني طرحتُ في محاضرة
"أساليب تعليم الرِّياضيَّات" فكرةَ صياغة منهاج يعتمد الألعاب بشكل
أساسيٍّ بحيث يمكن أن تُطرَح فيه عبارة: "لنلعب اللُّعبة الآتية" بدلاً
من صيغة السؤال المعهودة: "حلّ المسألة الآتية"! وقدَّمتُ في حينه أكثر
من مثال من أكثر من مرحلة تعليميَّة، وضمن مادَّة الرِّياضيَّات دومًا،
عن صياغة مسائل من قلب المناهج الحاليَّة في قالب لعبة أو مسابقة.
أمَّا محاضرة المناهج المدرسيَّة وعلوم الفضاء فقد عرضت فيها
للإمكانيَّات الكبيرة والهامَّة لإدراج فقرات، إن لم يكن مادَّة
بذاتها، لمواضيع تخصُّ الفضاء وترتبط بالرِّياضيَّات والفيزياء
والمعلوماتيَّة والعلوم وأيضًا بالتَّاريخ والفلسفة وغيرها من المواد
وصولاً إلى الإشارة إلى الأهمِّيَّة البالغة لدور أدب الخيال العلميِّ
ومركزيَّة موضوع ريادة الفضاء فيه. وأشرتُ إلى الأهمِّيَّة التي ينطوي
عليها هذا الطَّرح باعتبارنا ندخل، على المستوى العالميِّ، عصر إنسان
الفضاء الذي يكتشف كواكب جديدة والذي يبحث عن كائنات عاقلة غير أرضيَّة
يمكن أن يلتقي بها في أيَّة لحظة...
اسمحوا لي أخيرًا أن أشدِّد على أنَّ هذا المسعى بجملته ينطلق أساسًا
من قناعتي بأنَّ إعادة النَّظر في المناهج المدرسيَّة وفي الأولويَّات
التَّعليميَّة التَّربويَّة أمرٌ لا بدَّ منه في مرحلةٍ تاريخيَّة
نعيشها لا على صعيد محلَّيٍّ فحسب بل على مستوى الأرض قاطبةً، وهذا
أمرٌ سبق أن شرحته في مقالةٍ نُشِرت في مجلَّة المعرفة الصَّادرة عن
وزارة الثقافة تحت عنوان التَّعليم والتعلُّم آراء ورؤى لمن
يحبُّ الرُّجوع والاطِّلاع[2].
واقعٌ متجذِّر:
يتآلف أبناؤنا على مرِّ الأعوام، ومن خلال دراساتهم للمواد العلميَّة،
مع عباراتٍ من قبيل: "مع إهمال مقاومة الهواء"، "باعتبار تسارع
الجاذبيَّة الأرضيَّة يساوي 10"، "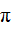 تساوي 3.14"، "دون أخذ الاحتكاك بعين الاعتبار"، "نسقط الفاصلة
العشرية" الخ... فهي عبارات يتواتر ورودها في مناهج الفيزياء
والرِّياضيَّات، ولكم هي قريبة من قلوب المدرِّسين قبل الطلاب!
تساوي 3.14"، "دون أخذ الاحتكاك بعين الاعتبار"، "نسقط الفاصلة
العشرية" الخ... فهي عبارات يتواتر ورودها في مناهج الفيزياء
والرِّياضيَّات، ولكم هي قريبة من قلوب المدرِّسين قبل الطلاب!
يُنظَر إلى مثل هذه العبارات على أنَّها أساسيَّة ولا غنى عنها في كلِّ
الفيزياء التَّقليديَّة، فعند دراسة حركة كرة حديدية تسقط سقوطًا حرًّا
(على سبيل المثال)، تُعتبر الجاذبيَّة القوَّة الرئيسيَّة التي تخضع
لها الكرة أمَّا مقاومة الهواء فهي قوَّة صغيرة أمام الجاذبيَّة ولا
يشكِّل إهمالها فارقًا يُذكَر...
هل ينفصل العلم عن التَّربية؟ هل يمكن لمثل هذا السُّلوك على مستوى
تناول قضايا علميَّة أن يلقي ظلاًّ أو آخر، ولأقل بصراحة: أن ينعكس
سلبًا، على الصَّعيد التَّربويِّ؟!
لنأخذ حالة واقعيَّة جدًّا... ينام معظم النَّاس وفي بيوتهم أجهزة
كهربائيَّة لم تُطفَأ نهائيًّا... حين لا نسحب قابس "التلفزيون"
و"الرسيفر" و"الميكرويف".. وغيرها من الآلات الكهربائيَّة الموجودة في
كلِّ منزل، وعندما يبقى هناك ضوء صغير أخضر أو أحمر في كلِّ جهاز،
فإنَّ هذا يعني أنَّ هناك دارة كهربائيَّة بسيطة تبقى في حالة العمل،
وأنَّ كلَّ منزل يهدر قدرًا ولو ضئيلاً من الطَّاقة، وإذا جمعنا هذه
الطَّاقة المهدورة في جميع المنازل معًا، على مستوى المدينة، بل في
كلِّ المدن لرأينا أنَّ البلد بمجمله يهدر طاقة لا يُستهان بها... وإذا
سأل أيُّ واحدٍ منَّا نفسه لماذا ندع هذه الطَّاقة تُهدَر سيجيب
ببساطة: هل يقف الأمر عليَّ وحدي أو: هل يؤثِّر عدم إطفاء التلفزيون
على صرف الكهرباء؟!...
أمَّا السُّؤال الذي أودُّ طرحه هنا فهو من مستوىً آخر: هل هناك علاقة
بين اعتياد الطلاب على التَّقريب (إهمال الاحتكاك، إهمال مقاومة
الهواء، وعمومًا إهمال المؤثِّرات الضَّئيلة...) وبين سلوكنا المتهاون
في الهدر والتَّبديد؟
ولكن، ومن جهة أخرى: هل صحيح أنَّه لا بدَّ من التَّقريب، ومن إهمال
الأمور الثَّانويَّة عند القيام بدراسة فيزيائيَّة أو رياضيَّة
معيَّنة؟ ربَّما نعم ولكن علينا أن نتذكَّر أنَّنا نتحدَّث هنا ضمن
الفيزياء التَّقليديَّة أو الفيزياء النيوتونية...
لنرتب أفكارنا كما يلي...
لا بدَّ لنا من دراسة الحركة كما ورثناها عن نيوتن، كونها من جهة أولى
تشرح ظواهر طبيعيَّة كثيرة [حركة الكواكب – سقوط تفاحَّة عن شجرة...]
وكونها تجد تطبيقاتها في ظواهر "بشريَّة" متعدِّدة [هندسة الطّرق –
مسارات القذائف، الخ...].
لا بدَّ من أجل ذلك من استخدام عبارات من قبيل نهمل الاحتكاك، ونهمل
مقاومة الهواء... وعلى العموم، لا بدَّ من أجل دراسة الميكانيك
النيوتوني من افتراض عزل الجسم الذي ندرس حركته عن كثير من الأشياء
التي تؤثِّر عليه حقيقة إنَّما بشكل محدود أمام قوى أهم في تأثيرها[3].
ينشِّئ هذا الأمر أولادنا من غير أن نقصد أو يقصدون على الاستخفاف
بالأمور الصغيرة وينعكس هذا على السُّلوك العامِّ هدرًا أو استخفافًا.
نحن في حلقة مفرغة إذًا: إنَّ دراسة العلم بشكل منهجيٍّ يسهم عن غير
قصد في تنمية ضربٍ من سلوك غير سويٍّ، مؤذٍ إن جاز القول، وعلينا أن
نجد حلًّا لهذه المعضلة! لا شكَّ أنَّ الأمر يتطلَّب تربيةً موازية
تنطوي على تنبيهٍ وتدريبٍ سلوكيٍّ مناسب، وهذا مسار بحث آخر. لكنِّي
أريد أن أقف عندما شرحته أعلاه لأقول، وهذا بيت القصيد، إنَّه يبدو لي
مثالاً بسيطًا عن قضيَّة أكبر بكثير.
مع بروز تأثير العلم، منذ عصر الثُّورة الصناعيَّة، وفرض ذاته منهجًا
يشرح الطَّبيعة ويفرض رؤية لا مفرَّ أمام مستخدمي منجزات التقنيَّة من
الأخذ بها... صار للعلم ولِنَقْلِ العلم (أي التَّعليم) دورٌ في توجيه
وتطوير سلوكنا من حيث ندري أو لا ندري. إنَّ المثال الأهمَّ الذي طرحه
أكثر من مفكِّر كبير هو علاقة الميكانيك النيوتوني وفق النظرة
اللابلاسيَّة بسلوكنا المنطوي على الآليَّة وهو ما يطبع جميع مجالات
حياتنا ويغيِّب الرُّوحيَّ والنَّفسيَّ لصالح المادِّيِّ والمحسوس،
فأيٌّ منَّا لم يبرِّر سلوكًا خاطئًا في يوم من الأيام بكونه "ردُّ
فعل" على خطأ غيره؟ إنَّ عبارة "ردُّ فعل" هي مصطلح فيزيائيٌّ
نيوتونيٌّ مائة بالمائة...
أعيد الاستشهاد بعبارة للفيزيائيِّ والفيلسوف بازاراب نيكوليسكو:
لقد صِيغَت الأفكارُ الاجتماعية والاقتصادية التي تَرجَحُ كفَّتها في
أيامنا هذه، عن وعيٍ أو عن غير وعي، وِفقَ رؤيةٍ للعالم مؤسَّسةٍ على
العلم في القرن التاسع عشر. حتَّى إنَّ أدقَّ أفعالِنا في الحياة
اليومية تُحدَّد إلى درجةٍ كبيرة بموقفِنا أمامَ الواقع، المتأثِّر
بدوره، وبالضرورة، ببيئتنا الثقافية.
ثمَّة تأخُّرٌ لا يكُفُّ عن التفاقم في دخولِ الأفكار العلميَّة إلى
حياتنا الفرديَّة والاجتماعيَّة. وقد يكون الأوان قد حان لدمج أفكار
العلم المعاصر على نحوٍ أكثر فاعليةً في ثقافتنا.
نسمع في الإعلام على سبيل المثال والتَّوضيح عبارة "توازن القوى" إذ
ثمَّة من يزعم أنَّ وقاية الأرض من حرب نوويَّة مدمِّرة يمكن أن يتمَّ
عن طريق توازن القوَّة النَّوويَّة بين معسكرَين متعارضَين. إنَّ عبارة
"توازن القوى" هي عبارة مأخوذة حرفيًّا من ميدان الفيزياء. لكن الذين
يستخدمونها دعمًا لمراكمة التَّرسانات النَّووية يغضُّون طرفهم عن
معرفة أو عن غير معرفة عن وجود نوع من التَّوازن في الفيزياء يسمَّى
"التَّوازن القلق" وهو عرضة للاختلال لأدنى سبب.
نعلم اليوم من جهة أخرى أنَّ عبارة "توازن القوى" في الفيزياء ليست
بمنأى عن فكرة إهمال القوى الصَّغيرة كما تحدَّثت أعلاه، كما نعلم
أيضًا أنَّ هذه القوى الصَّغيرة التي يهملها الميكانيك التَّقليديُّ
يمكن أن تتضخَّم لتصبح على المدى الطَّويل مؤثِّرة جدًّا وأساسيَّة،
وهو ما ينصُّ عليه مبدأ "مفعول الفراشة" الذي بدأ يدخل أدبيَّات
الفلسفة أيضًا بل يكاد حتَّى أن يصبح مصطلحًا إعلاميًّا شائعًا.
أيُّ تغييِّر في التَّعليم نريد؟ ما الذي يمكن أن يضمن "خلاص" العالم
حقًّا؟!
حين يقرأ أحدنا روايةً أو مجموعة قصصيَّة تتضمَّن حكمة هادفة، أو حين
نشاهد فيلمًا يرمي إلى إيصال فكرة معيَّنة، أو حتَّى حين نحضر محاضرة
علميَّة بحتة، فإنَّنا على الأغلب نعلِّق في نهاية الأمر بإحدى
العبارتين: "جميلة"، "غير جميلة". فنحن في نهاية الأمر نهتمُّ من العمل
الأدبي أو الفنيِّ أو حتى العلميّ بما تركه في نفسنا من أثر جميل أو
غير جميل أكثر ممَّا تركه في فكرنا من معلومات.
"الجمال وحده هو الذي يمكن أن يخلِّص العالم"، يقول دوستويفسكي، ذلك
الرُّوائيُّ العظيم، والرَّائي الكبير أيضًا!
إنَّ مبدأ مفعول الفراشة، الذي ذكرته قبل قليل، هو ركنٌ هامٌّ في
نظريَّة الشَّواش، وهي نظريَّة ترتبط ارتباطًا وثيقًا بالهندسة
الكسوريَّة.
يقول روبرت ماي أحد مهندسي نظريَّة الشَّواش:
إنَّه لمنَ الواجبِ تدريسُ الشواش. لقد أتى الوقت الذي بات علينا أن
نعتقد فيه بأنَّ التعليم التقليديَّ يُساعد على ارتكاب الخطأ في
الحكم... إنَّ من الممكن لكلِّ شيء أن يسيرَ على نحوٍ أفضل، لا على
صعيد البحث العلمي فحسب بل وعلى صعيد الحياة اليوميَّة أيضًا، إذا
ازدادَ وعيُ الناس لواقع أن الجُملَ اللاخطيَّة الأساسية لا تملك
بالضرورة خصائص حركية بسيطة.
وروبرت ماي ليس الوحيد، إذ ترتفع أصوات بين العلماء وفلاسفة العلم تدعو
إلى تربية جديدة تأخذ بعين الاعتبار جديد العلوم ولا سيَّما ما تطرحه
نظريَّات الميكانيك الكوانتيِّ والشَّواش والهندسة الكسوريَّة التي
سنتوقَّف عندها اليوم، كونها ذلك الفرع من الرِّياضيَّات الذي يقدِّم
لنا من بعض ما يقدِّم بعض آيات الجمال!
أودُّ أن أعيد القول موجِزًا: إنَّ الغاية الأساسيَّة - دون إنكار وجود
غايات أخرى - من طرحي لربطٍ بين الهندسة الكسوريَّة والمناهج
المدرسيَّة هو تربية حسِّ الجمال، مع طرح رابطٍ بين نظريَّاتٍ حديثة في
العلم يمكن أن تربِّي ضربًا من السُّلوك أكثر إيجابيَّةً بمعنى ما.
يمتنع الرِّياضيُّ الكبير، بونوا ماندلبروت، رائد الهندسة الكسوريَّة،
وناحت مصطلح "فراكتال" التي يغلب تعريبها بـ "كُسَير" عن إعطاء تعريف
محدَّد له. هذا سبب إضافيٌّ يجعلني أتجاوز محاولة شرح ما هي الهندسة
الكسوريَّة [لا سيَّما أنَّ الموضوع طُرِح أكثر من مرَّة على منبر هذه
الجمعيَّة، وفي العديد من المنتديات التي تُعنى بتبسيط أو فلسفة
العلوم...] إلى طرح بعض القضايا التي يمكن بكلِّ بساطة أن تكون مواضيع
لأحاديث أو أنشطة صفّيَّة مع مجموعات من التَّلاميذ والطَّلبة في مراحل
دراسيَّة مختلفة لكي يلامسوا بأنفسهم هذا الفرع من الرِّياضيَّات من
جهة ولكي يحتكّوا بما فيه من جمال من جهة أخرى. وأظنُّ أنَّ من الممكن
من خلال هذه الأمثلة أن يكوِّن كلُّ واحدٍ لنفسه فكرة عمَّا هي الهندسة
الكسوريّة [إن لم يكن قد تعرَّف إليها من قبل].
أنشطة صفّيَّة
نشاط أول
يمكن أن يُطلبَ من تلاميذ في المرحلة التَّحضيريَّة أي ما قبل المدرسة
تلوين بعض الصُّور من النَّمط التالي:
[يمكن القيام بذلك عن طريق توزيع أوراق مطبوعة فقط، أو توزيع نماذج
ملوَّنة مع الرُّسوم المطلوب تلوينها، أو باستخدام برنامج (الرَّسَّام)
أو ما شابه على الحاسوب...]



ليس المطلوب هنا تقديم شروح. سوف يلوِّن الأطفال هذه الأشكال. سيشعرون،
وهم الأكثر ذكاءً وإدراكًا للجمال ممَّا نتصوَّر، بوجود نوعٍ من
الـ"تناظر" أو التِّكرار دون أن يستطيعوا تسميته. وسيكون ذلك تحضيرًا
لأشياء تأتي فيما بعد.
نشاط ثانٍ
يمكن أن يُطرَح هذا النَّشاط مع تلاميذ في الصَّفِّ الثَّاني من مرحلة
التَّعليم الأساسيِّ. إنَّه نشاطٌ فنِّيٌّ كما هو واضح. وأهمُّ ما فيه
هو الوصول إلى حالة يُدهَش معها التَّلاميذ لنتيجة ما صنعت أيديهم وهذا
أمرٌ مهمٌّ بحدِّ ذاته. في هذه المرحلة يمكن أن نستخدم صراحة اسم العمل
الذي يقوم به التَّلاميذ [وهو التَّكرار
Iteration]
ويمكن أن يُفهَم المصطلح من خلال تطبيقه عبر هذا النَّشاط كما يمكن طرح
أمثلة أخرى مشابهة.
وأغلب الظنِّ أنَّ بعض التَّلاميذ سيسألون: "كم من المرَّات يمكننا
القيام بهذا التَّكرار"؟ وستكون فرصةً للتَّحدُّث عن مفهوم اللانهاية
أيضًا، وهو مفهوم يراود أذهان الأطفال بحسب ما تؤكِّد الكثير من
الأسئلة التي يطرحونها.
|
يأخذ التلميذ قطعة من الورق المقوّى ويطويها ثم يرسم خطًا
في منتصفها على النحو الموضَّح |

|
|
يقص التلميذ الورقة بحسب الخط المرسوم. |

|
|
تُطوى الورقة في مكان القص ثمَّ تفرد من جديد لتبدو على
هذا الشكل. |

|
|
يعاد طي الورقة وتُرسَم خطوط على النحو الموضح في الشكل.
ثم تعاد عملية القص والطي مرة أخرى. |

|
|
|

|
|
ستبدو قطعة الورق المقوى بعد نشرها على الشكل التالي.
وتُعاد العملية كرَّة أخرى. |

|
|
|

|
|
أخيرًا يمكن قلب الشكل ليبدو كما يلي:
(يمكن للاستعانة بخلفية من لون آخر أن يعطي انطباعًا
أجمل...) |
 |
من المهمِّ جدًّا قبل أن أتابع تقديم هذه الأنشطة أن أشدِّد على كونها
أمثلة من مجموعة أوسع يمكن أن تشكِّل على نحوٍ مدروس سلسلةً متتالية
على مرِّ السَّنوات والحلقات الدراسية وليست أنشطة منفصلة.
نشاط ثالث
يمكن لهذا النَّشاط أن يكون متعدِّد الأهداف، أي أن يكون الجانب
الكسيريُّ فيه هدفًا من بين عدَّة أهداف أخرى. وهو نشاطٌ يمكن أن يجري
بطريقة ما ضمن المدرسة (بحسب مكانها وطبيعتها) أو عبر الصُّور والعروض
التَّفاعليَّة. والأفضل أن يكون خلال رحلة في رحاب الطَّبيعة ويمكن
تصميمه بتصرِّف ليكون مناسبًا لأيِّ عمر بين السَّابعة والثَّانية
عشرة.
بعد شرح لفكرة "التَّماثل الذَّاتيِّ"، أو "التَّشابه على سلالم القياس
المتعدِّدة"، وهي الفكرة التي سبق أن اختبرها التَّلاميذ في أنشطة
وسنوات سابقة، وبعد إعطاء بعض الأمثلة المختلفة الطَّبيعيَّة وغير
الطَّبيعيَّة عن الفكرة، يمكن أن يُطلَب إلى التَّلاميذ، خلال رحلة في
الطَّبيعة، تأمُّل الغيوم أو الأشجار أو الأرض (التُّراب) أو أوراق
الأشجار... والبحث في كلِّ ما يصادفونه عن أشياء تشبه أجزاءها. كما
يمكن أن يُطلَب منهم تسجيل ملاحظاتهم كتابيًّا أو رسمًا أو تصويرًا (ما
دمنا في عصر التكنولوجيا للجميع!)
إنَّ هذا النَّشاط بشكل خاصٍّ، يمكن أن يكون مصدرًا غنيًّا للمعلِّم أو
المدرِّب، كما للأهل، في عمليَّة تمييز قدرات ومواهب أولادهم. واسمحوا
لي مرَّة أخرى أن أشير هنا إلى أنَّني تحدَّثت في المقالة المُشار
إليها أعلاه عن أهمِّيَّة التَّمييز الصَّحيح للمواهب إلى حدِّ أنِّي
اعتبرتُ أنَّ مرحلة التَّعليم الأساسيِّ (حتَّى سنِّ الـ 15 تقريبًا)
بكاملها يمكن، ويتوجب أن تكون، مرحلة تمييز لمواهب الطِّفل وتوجيه نحو
اكتشافها ومعانقتها. إنَّ ما يمكن أن يبديه التَّلامذة من ملاحظات،
والطَّريقة التي يختارونها لصياغة هذه الملاحظات، وكذلك ما يمكن أن
يطرحوا من أسئلة وما يستخدموا من أدوات تنطوي على إشارات هامَّة لملكات
واستعدادات كلِّ واحد منهم. ولا بدَّ من الإشارة هنا إلى أن مثل هذه
الأنشطة تتطلب مرونة كبيرة في التَّعامل كما تتطلَّب ألا تُحصر في
نتائج محدَّدة سلفًا يتوقَّع المدرِّس الحصول عليها ويقيِّم التَّلاميذ
من خلالها بطريقة تقليديَّة.
|
 |

|
 |
|
 |
 |
 |
|
في جميع الأشكال الطبيعية السابقة يمكن ملاحظة نوع من
التماثل الذاتي ويمكن أن تُشرح الفكرة ببساطة كما يلي: إذا
أخذنا جزءًا من الصورة وكبَّرناه إلى مساحة الصورة الأصلية
فسنحصل على صورة جديدة تشبه "تمامًا" الصورة الأصل. |
نشاط رابع
ما سيجري عمليًّا هو الانطلاق من هذا الشَّكل البسيط (وسنسمِّيه وحدة
أوَّليَّة) أو من مكوِّناته:

للوصول إلى هذا المجسَّم المركَّب:

ولعلَّ من الواضح أنَّه يمكن تركيب المزيد من القطع وصولاً إلى شكل
أعقد. يمكن وصف النشاط إذًا على النحو التالي: يتشارك صفٌّ بكامله (بين
9 و11 سنة) في صناعة مثل هذا المجسَّم الكسيري وذلك بدءًا من عدد من
المركِّبات الأوليَّة.
سوف يُقسَّم التَّلاميذ إلى مجموعات بحيث تضمُّ كلُّ مجموعة خمسة
أعضاء. ضمن كلِّ مجموعة، يصنع كلُّ تلميذ بمفرده هرمًا واحدًا مركَّبًا
من خمس وحدات أوَّليَّة، ثمَّ تقوم المجموعة بضمِّ الإهرامات الخمسة
لصنع هرم مركَّب أكبر مؤلَّف من خمس أهرامات مركَّبة. أخيرًا تشترك
المجموعات (خمس مجموعات) لتركيب هرم أكبر، ويمكن أخيرًا إذا أردنا أن
يشترك خمسة صفوف (عدد طلاب كل صف منها 25) لصنع هرم عملاق رائع.

ويحتفل الأولاد بإنجازهم الفنِّيِّ الجماعيِّ.
أظنُّني لا أستطيع أن أتحدَّث كثيرًا عن الغنى التَّربويِّ
والتَّعليميِّ في مثل هذا العمل، فهو أوضح من أن أتحدَّث عنه. أشير
فحسب إلى أنَّه يمكن التحكُّم بحجم هذا العمل بحسب عدد التَّلاميذ في
الصَّف وبحسب الوقت الذي يُعطى للقيام به. بمعنى أنَّ تصميم النَّشاط
يمكن أن يتيح قدرًا كبيرًا من المرونة للمشرف أو المعلِّم.
إنَّ إنجاز هذا العمل يمكن أن يكون مقدِّمةً لشرح مجسَّم رياضيٍّ شهير
يسمَّى هرم سيربنسكي ويمكن عرض الأمر على النَّحو الآتي:
|
ليكن لدينا هرمًا رباعيًّا منتظمًا يشبه أهرامات الجيزة
الشهيرة. |

|
|
يمكن من حيث المبدأ، كما يمكن عمليًّا تفريغ الشَّكل
السَّابق من الدَّاخل بحذف هرم رباعيٍّ (مقلوب – أي قاعدته
إلى الأعلى) من داخل الهرم السابق، كما هو موضح في
الصُّورة. وسنحصل على شكل مؤلَّف من 5 أهرامات يشبه كلٌّ
منها الهرم الأصلي ولكنه أصغر حجمًا. |

|
|
نكرِّر عمليَّة التَّفريغ التي قمنا بها على الهرم الأصلي
على كلٍّ من الأهرامات الخمسة الأصغر فنحصل على المجسَّم
الموضح في الصورة التالية، المؤلَّف من خمسة أهرامات كلُّ
منها مفرَّغ بحيث يعطي خمسة أهرامات صغيرة أيضًا. |

|
|
نشير إلى الصُّورة الأولى من هذه السِّلسلة أي صورة الهرم
الكامل بالمرحلة 0 (أي أنَّنا لم نقم بأي حذف بعد) ونشير
للصورة الثانية بالمرحلة 1 وهكذا... الشكل المجاور إذًا هو
المرحلة 3 وفيه 125 هرمًا صغيرًا. |

|
|
وفي المرحلة الرابعة سيكون لدينا مجسَّمًا مؤلَّفًا من 625
هرمًا صغيرًا (ينتج هذا العدد من ضرب العدد 5 بنفسه أربع
مرات). |

|
|
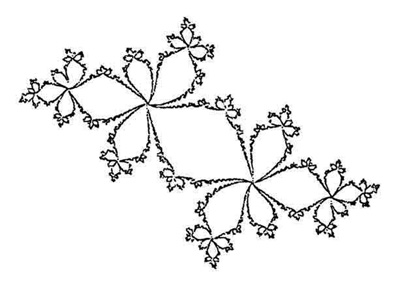
توضح لنا هذه الصورة إنَّنا لو نظرنا إلى الشكل السابق
(المرحلة الرابعة) من بعيد فإنِّنا لن نلحظ التفاصيل بل
سنرى كما لو أنَّ الشكل هو المرحلة 2. وبطبيعة الحال لو
نظرنا من أبعد فسنرى مجرد هرم كامل. |
 |
يملك الدِّماغ البشريُّ (وهو الأمر الذي ما يزال يميِّزه عن أفضل
منتجات الذَّكاء الصُّنعيِّ) إمكانية أن يتخيَّل استمرار العمليَّة على
نحوٍ لانهائيٍّ. وفي هذه الحالة سنحصل على مجسَّم يبقى لانهائيًّا إذا
اقتطعنا جزءًا منه وهنا نرى التَّماثل الذَّاتيَّ بصورته الكاملة الأمر
الذي لا نراه في الواقع وإن كنَّا نرى تقريبات له في تكرارات منتهية
العدد.
يمكن الإشارة هنا، وهذا أمرٌ يُفهم من قبل الطلاب، أنَّنا مع كلِّ
تكرار (تفريغ للأهرامات) نحصل على مجسَّم جديد واقع ضمن حجم محدود
(طالما أنَّه أصغر من حجم الهرم الأصلي) لكنَّه يزداد مساحة مع كلِّ
تكرار (لأنَّ المساحة الجانبية للأهرامات الخمسة الناتجة أكبر من مساحة
الهرم الواحد الناتجة عنه). يعني هذا من حيث المبدأ إمكانية حشر مساحة
كبيرة بقدر ما نريد داخل حجم محدود. وهذا في الواقع ما تفعله الطَّبيعة
في أمثلة عديدة أشهرها أنَّ المساحة التي يتفاعل فيها سطح قصباتنا
الهوائيَّة وتفرُّعاتها في الرِّئتين مع الهواء الدَّاخل والخارج إلى
الجسم تعادل مساحة ملعب كرة المضرب لكنها محشورة، من خلال بنية
كسيريَّة مشابهة من حيث المبدأ لما شرحناه أعلاه، ضمن حجم الرئتين
الصَّغير.
يُسمَّى الشكل السَّابق هرم سيربنسكي، ومن الواضح أنَّ العمل الذي قام
به الطلاب هو المجرى المعاكس لإنشاء هرم سيربنسكي، فهم قاموا بعمليَّة
تركيب بدل التَّفريغ. لكنهم سيرون مراحل إنشاء هرم سيربنسكي السَّابقة
لاحقًا بل ويمكنهم أن يتعلَّموا أيضًا كتابة برنامج لتوليد هذه الصُّور
وهنا نرى ربطًا مع مادَّة المعلوماتية التي تقتصر في كثير من الأحيان،
ومع الأسف، على تعلُّم برامج جاهزة.
نشاط خامس
يدرس الطلاب في الصف الثامن أو التاسع المبرهنة الشهيرة لفيثاغوراس.
أودُّ أن أشير هنا إلى أنَّ هذه المبرهنة مع اسم صاحبها يمكن أن تشكِّل
مدخلاً لغنىً كبير للطلاب يتراوح بين الرياضيات والتاريخ والفلسفة
والموسيقا وغيرها، فمعظم الذين سمعوا بمبرهنة فيثاغوراس لا يعرفون أنَّ
المذكور كان مفكِّرًا صاحب مدرسةٍ روحيَّة وموسيقيًّا وفيلسوفًا إلى
جانب، وربَّما قبل كونه عالم رياضيَّات. بيد أنَّ شيئًا من مثل هذا
الطرح لا يؤخذ بعين الاعتبار. وأعيد التذكير بأنَّني أتحدَّث على نحو
عام أوسع من محلي.
وبالعودة إلى ما يخصُّ استخدام مبرهنة فيثاغوراس مدخلاً إلى نشاط
فراكتالي يمكن للطلاب أن ينطلقوا من رسم بسيط:
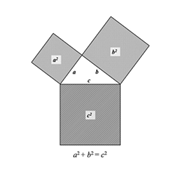
ثمَّ يقوموا بمعاودة العملية مرات عديدة:
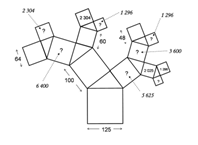
يمكنهم لاحقًا استخدام برنامج حاسوبي وهناك أكثر من برنامج يمكن الحصول
عليه بيسر لتكرار العملية عددًا كبيرًا من المرات وسيرون في النتيجة
شكلاً من هذا النحو:
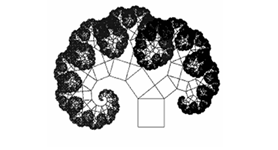
في إحدى المدارس جرى طرح السُّؤال التالي على الطلاب: ما الذي يشبهه
هذا الشكل؟ أجاب بعضهم: الدِّماغ. وأجاب آخر: زهرة القرنبيط وأجاب
آخرون الحلزون. مرَّة أخرى نرى هنا وسيلةً فعَّالة للتَّعرُّف على
الطلاب وكيفية تناولهم للأمور والملفت للنَّظر أنَّ كلاً من القرنبيط
والحلزون والدماغ لها بنى فراكتالية واضحة.
نشاط سادس
[لطلاب من الفرع العلميِّ (ما يوازي الصف الحادي عشر العلمي في
المنظومة التربوية في سورية)]
نشاهد هنا المزيد من الارتباط مع الرِّياضيَّات ونستطيع أن نستخدم هذا
النشاط وسيلةً لتعريف الطلبة بفكرة البعد الكسيري مستخدمين معلومات من
ضمن منهاجهم.
لدينا مثلث متساوي الأضلاع نفرض أن طول ضلعه يساوي الواحد (الشكل الأول
من اليسار).
نقسم كلَّ ضلع إلى ثلاثة أجزاء متساوية.
نمحي القسم الأوسط من كلِّ ضلع (الجزء الملوَّن بالأخضر في الشكل
الثاني من اليسار)
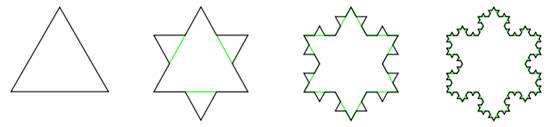
نرسم ضلعي مثلَّث متساوي الأضلاع يكمل كلُّ جزء منقوص (أخضر) فنحصل على
نجمة سداسيَّة كما هو واضح.
نعيد نفس المراحل على كل ضلع من أضلاع النجمة السداسية... ونستمر
بالتكرار بقدر ما نريد.
يدرس الطلاب في الصف الحادي عشر العلمي مبادئ المتتاليات والمتسلسلات
العددية، ويتعرَّفون على التمييز بين المتتالية المتقاربة والمتباعدة
ويتعلَّمون إيجاد مجموع متسلسلة (ضمن أمثلة معيَّنة من المتسلسلات).
يمكن أن تكون الأشكال أعلاه مدخلاً إلى هذا البحث مع كونها طريقة
للتَّعريف على البعد الكسيريِّ وذلك كما يلي:
يُطلَب من الطلاب إكمال الجدول التالي:
|
المرحلة |
0 |
1 |
2 |
3 |
………… |
N |
|
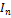 عدد
الأضلاع عدد
الأضلاع |
|
|
|
|
|
|
|
طول الضلع
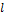 |
|
|
|
|
|
|
|
المحيط
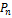 |
|
|
|
|
|
|
|
المساحة
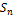 |
|
|
|
|
|
|
المرحلة صفر تعني المثلَّث قبل أي تعديل، والمرحلة 1 تعني النجمة
السداسية، الخ... سيكون على الطالب (ضمن مجموعة عمل مثلاً) أن يعرف عدد
الأضلاع في كل مرحلة، ثم طول الضلع (إذا فرضنا أنه يساوي الواحد في
المرحلة صفر) ثم يستنتج محيط الشكل ومساحته.
إن الوصول إلى المتغيرات السابقة في حالة المرحلة رقمn
يعني إمكانية أن يستنتج الحد العام لمتتالية بدءًا من معرفة بعض
حدودها الأولى. ومن الواضح هنا أن لدينا 4 متتاليات متدرجة في صعوبة
استنتاج حدها العامِّ.
سيكون الجدول لاحقًا على الشكل التالي:
|
المرحلة |
0 |
1 |
2 |
3 |
………… |
N |
|
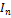 عدد
الأضلاع عدد
الأضلاع |
3 |
12 |
48 |
192 |
|
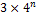 |
|
طول الضلع
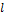 |
1 |
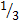 |
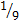 |
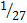 |
|
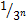 |
|
المحيط
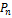 |
3 |
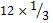 =
4 =
4 |
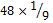 = =
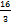 |
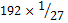 = =
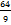 |
|
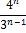 |
|
المساحة
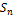 |
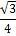 |
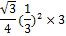 |
|
|
|
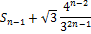 |
يمكن باستخدام معارف الطلاب عن المتتاليات والمتسلسلات أن يتوصَّلوا
إلى استنتاج أن المساحة محدودة بسبب تقارب المتتالية (كما يمكن استنتاج
ذلك هندسيًا كون المساحة محدودة ضمن المثلث الأصلي فهي أصغر من مساحة
هذا المثلَّث بالتّأكيد). أمَّا المحيط فمن الواضح أنه ينتهي إلى
اللانهاية وهو ما يمكن أن يتوصَّل إليه الطلاب بأنفسهم أيضًا.
يعني هذا وجود خطٍّ طوله لانهائيٌّ ضمن مساحة محدودة. ومن هنا يأتي
البعد الكسيريُّ: الخط الذي طوله لانهائي ولكنه يحصر مساحة محدودة هو
خطٌّ بعده أكبر من الواحد وأصغر من 2 وهناك تقنيَّات رياضيَّة تعطي هذا
العدد (البعد) من أجل كلِّ خطٍّ وفي حالة الشَّكل الذي ندرسه، والذي
يُسمَّى "منحني كوتش"، يمكن تبسيط فكرة حساب البعد الكسيري كما يلي:
عندما ننتقل من أحد الرؤوس إلى رأسٍ تالٍ له (أي نقطع ضلعًا كاملة) في
الشكل
n،
فإنَّنا نكون قد قطعنا 3 خطوات (3 أثلاث) وللانتقال بين نفس النقطتين
ولكن في الشكل
n+1
يكون علينا أن نتقدَّم 4 خطوات مماثلة. يُعطى البعد
الكسيري في هذه الحالة بالعلاقة:
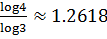
نشاط سابع
أختم مجموعة النَّشاطات (التي يمكن أن أذكر الكثير منها بعد) بفكرة
نشاط أخير مرتبط من جهة بالأعداد المركَّبة التي يدرسها طلاب الثانويات
العلمية أيضًا، ومن جهة أخرى بالمعلوماتية.
نعرِّف المتتالية العقديَّة (ضمن مجموعة الأعداد المركَّبة) بحدِّها
العام:
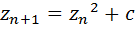
حيث:
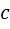 عدد مركَّب ثابت، وحيث
عدد مركَّب ثابت، وحيث
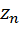 عدد مركب متغير.
عدد مركب متغير.
تختلف الأعداد المكوِّنة للمتتالية باختلاف قيمة الثابت
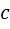 كما باختلاف الحد الأول الذي
نفترضه، أي
كما باختلاف الحد الأول الذي
نفترضه، أي
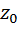 وتُسمَّى الحالة
وتُسمَّى الحالة
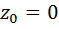 مجموعة ماندلبروت. وليكن
نشاطنا ضمن هذه الحالة.
مجموعة ماندلبروت. وليكن
نشاطنا ضمن هذه الحالة.
يمكن أن يختار كل طالب عددًا ثابتًا
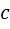 ويحسب بضعة حدود من المتتالية الناتجة، وهذا تمرين مفيد في استخدام
العمليات البسيطة على الأعداد المركَّبة.
ويحسب بضعة حدود من المتتالية الناتجة، وهذا تمرين مفيد في استخدام
العمليات البسيطة على الأعداد المركَّبة.
الفكرة التي يُراد الوصول إليها أنَّنا بحسب قيم الثابت نحصل على
متتالية متقاربة (محدودة) أو متباعدة (تسعى إلى اللانهاية). ويمكن طرح
أمثلة بالاستعانة بآلة حاسبة علميَّة أو بالحاسب الآلي.
في المستوي العقدي الذي يمثِّل المحور الأفقي فيه الأعداد الحقيقية
ويمثِّل المحور الشاقولي الأعداد التخيلية، يمكن القيام بما يلي: إذا
اخترنا عددًا ثابتًا
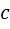 فحصلنا
على متتالية متقاربة فإنَّنا نمثِّل العدد
فحصلنا
على متتالية متقاربة فإنَّنا نمثِّل العدد
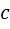 في المستوي الإحداثي (أي نضع فعليًّا نقطة) أمَّا إذا
كانت المتتالية متباعدة فإنَّنا نترك مكان العدد
في المستوي الإحداثي (أي نضع فعليًّا نقطة) أمَّا إذا
كانت المتتالية متباعدة فإنَّنا نترك مكان العدد
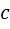 خاليًا.
خاليًا.
عمليًّا، لا يمكن الاستمرار في العلمية يدويًّا (مع أنَّ عالمًا
فرنسيًّا اسمه غاستون جوليا قد فعل ذلك في بدايات القرن العشرين) وهنا
يأتي دور الحاسب. يمكن أن يتعلَّم الطلاب وضع البرنامج اللازم للقيام
بهذه العملية، وهو برنامج بسيط نسبيًّا، وفي جميع الأحوال فإنَّ
استخدام هذا البرنامج سيكشف أنَّ مجموعة النقاط السوداء ستعطي شكلاً
مدهشًا هو التالي:

وهو شكل شبَّهه أحد علماء الرياضيات (إيان ستيوارت)[4]
بكعكة الزنجبيل أمَّا اسمه العلميِّ فهو: "مجموعة ماندلبروت".
أهمُّ ما في الموضوع هو أنَّ هذا الشكل يكشف عن مجموعة رائعة من
الأشكال عندما نكبِّر أجزاء منه، وفي قلب الشَّكل الأوَّل، أي عندما
نقوم بالتَّكبير عددًا كافيًا من المرَّات سنعود لنُفاجأ بالشَّكل الذي
انطلقنا منه وهنا نقع مرَّة أخرى في مثالٍ عن التَّماثل الذَّاتي. نرى
أدناه صورة توضح الفكرة ويمكن أن نجد في الرابط التالي تمثيلاً حركيًّا
للفكرة[5].

إنَّ توليد مجموعات وصور فراكتالية مثل مجموعة ماندلبروت من قبل الطلاب
أنفسهم سيكون من جهة أولى تطبيقًا معلوماتيًّا على بحث الأعداد
المركَّبة الذي يُطرَح - بطريقة شديدة التجريد وبعيدة كلَّيًا عن أيِّ
تطبيق - على طلاب الفرع العلمي. فيبدعون لوحاتهم الخاصَّة على الحاسب
باستخدام دوال عقديَّة، ويكونون مرَّة أخرى، عبر الرياضيَّات
والمعلوماتيَّة على تماسٍ مع الجمال. علَّ الرسالة تصل: إنَّ الجمال
نفع للنَّفس والرَّوح، وإنَّ الجمال كافٍ باعتباره غاية، وإنَّ
الرياضيات غير بعيدة عن الجمال.
سبق أن صرَّح ماندلبروت بأنَّ الفراكتال رياضيات صرفة ساعد في تبلورها
تطور الحواسب الحديثة والسريعة. وهذا صحيح بكلِّ تأكيد فلقد سبق العالم
الفرنسي جوليا خلفه ماندلبروت في إنتاج بعض الرسوم الفراكتالية يدويًا.
لكن هذا الغنى الكبير لم يكن ممكنًا بدون وسائل المعلوماتية الحديثة.
وفي هذا البحث تحدَّثت كثيرًا عن إمكانيات دمج الهندسة الكسوريَّة في
المناهج دون أن أتطرَّق بعمق إلى المدى الرَّحب الذي يزداد أكثر فأكثر
فيما لو تمَّ استخدام الأدوات المعلوماتيَّة الحديثة ضمن المدرسة
فمادَّة المعلوماتيَّة يمكن أن تشكِّل بيئة ملائمة جدًّا لاستخدام
برامج الفراكتال الجاهزة بقدر ما لكتابة برامج فراكتاليَّة من قبل
الطلاب أنفسهم، وفي مختلف المراحل والصفوف الدراسية... إنَّ عنوانًا من
قبيل "المعلوماتيَّة والهندسة الكسوريَّة في المناهج المدرسيَّة" يمكن
أن يكون موضوعًا مستقلاً قد يحالفني الحظُّ لطرحه في مرَّة قادمة.
أودُّ فيما تبقى أن أقدِّم مثالاً مختلفًا عن إمكانية رؤية الهندسة
الكسوريَّة في البنية التَّربوية نفسها. وأنطلق من أجل ذلك من المثال
التالي:
لدينا مثلث متساوي الأضلاع.
نقص من المثلَّث مثلَّثًا داخليًّا متساوي الأضلاع أيضًا، كما في
الشكل...
يبقى لدينا شكل مؤلف من أربعة مثلثات تشابه المثلث الأصلي.
نعيد العملية على كلِّ مثلَّث من المثلَّثات الثَّلاثة السابقة:
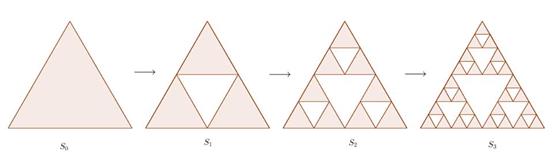
نتخيَّل إعادة العملية عددًا لانهائيًا من المرات...

ما هو الشكل الذي لدينا؟ إنه شكل متماثل ذاتيًّا، شكل يشبه، بل يكافئ
جزء منه الشكل كله. (يسمَّى هذا الشكل مثلَّث سِربينسكي).
ماذا يعني ذلك. يعني أنَّه شكل ثابت. ماذا يعني ثابت؟ يعني جامد؟ ماذا
يعني جامد؟ يعني بلا حياة.
كيف يتغيَّر هذا الشكل، كيف ننتقل من هذا الشكل إلى شكل آخر؟ عندما
نقوم في مرحلة من المراحل (اللانهائية) بتغيير القاعدة، عندما ننسى
قصَّ أحد المثلَّثات مثلاً، أو عندما نبدع عمليَّة جديدة أيًّا كانت؛
هل يذكِّرنا هذا بفكرة "الطَّفرة" في التطوُّر؟
دونكم الغيوم على سبيل مثالٍ يأتي من الطبيعة...
كان يحلو لماندلبروت أن يردِّد مقولته الشهيرة:
الغيوم ليست كرات وما الجبال بمخاريط.
والحقيقة هي أنَّ للغيوم بنية فراكتاليَّة أيضًا. ولكن، متى يهطل
المطر؟! حين، لسببٍ ما، تُكسَر في مكانٍ ما هذه البنية!
لنأخذ مثالاً أكثر ارتباطًا بحياة الناس، وسأروي قصَّةً افتراضيَّةً
بقدر ما هي قصَّة كلِّ يوم:
تعيد المعلِّمة عشر مرات شرح الفكرة لكن الطالب "سين" لا يفهم. يوضح
المدير للمعلِّمة عشر مرات - كما كان قد سبق أن أوضح لتسع معلِّمات
غيرها - أنَّ الطالب لن يفهم ولو أعادت الشَّرح عشر مرات لأنَّها تعيد
الشَّرح نفسه، بالكلمات نفسها، ولا تجد طريقة جديدة لإعادة الشَّرح من
منظورٍ جديد، أو من زاويةٍ جديدة تناسب إمكانيَّات أو طريقة تفكير هذا
الطالب بالذات. لكن المعلمة، ورفيقاتها التسع، لا يستطعن فهم ما يطلبه
منهنَّ المدير الذي يشكو مشكلته إلى الموجه الاختصاصي. يقوم الموجه
الاختصاصي بواجبه على أكمل وجه: يعيد على مسامع المدير، وللمرَّة
العاشرة، ما كان قد أعاده على تسعٍ من المدراء الآخرين - عشر مرات لكل
واحد منهم - مكرِّرًا حرفيًّا مقولته الذهبيَّة: يا أخي أنت سيِّد
العارفين... عليك أن تجد الطَّريقة المناسبة لإيصال فكرتك إلى هذه
المعلِّمة أو تلك، فهنَّ لسن جميعًا سواء. ولا يتعلق الأمر أبدًا بعدد
المرَّات بقدر ما يتعلَّق بالأسلوب. ومع كلِّ هذا الجهد الذي بذله
الموجِّه الاختصاصي، ومع نجاحه في صياغة توصيته بعبارة واضحة دقيقة لا
مجال لتأويلها، بيد أنَّ السَّادة المدراء لم تصلهم الفكرة. الأمر الذي
لاحظه الخبير التَّربويُّ العام، لا في القطاع الذي يشرف عليه هذا
الموجِّه الاختصاصيُّ فحسب، بل في تسع قطاعات أخرى مماثلة، فكان عليه
أن يقول عشر عشر مرات إنَّ....
ماذا يعني هذا الأمر؟ مَن المسؤول عن عدم فهم الطالب؟ المعلِّمة، أو
المدير، أو الموجه الاختصاصي أو الخبير التربوي الأعلى؟
كلهم يتحملون نفس المسؤولية تمامًا لأنهم كلهم يرتكبون نفس الخطأ
بالذات. كيف نصل إلى النتيجة المرجوة: أن يفهم الطالب؟ بأن يكسر أحد
أعضاء السلسلة هذا الإيقاع، أي عندما يقوم بشرح فكرته بطرق مختلفة حقًا
بدلاً من تكرار العبارة ذاتها على الجميع. ما معنى ذلك؟ معنى ذلك أن
العملية التربوية لا تبدأ بتصحيح مسارها إلا حين يخرج أحد ما من أي
مستوى كان عن القاعدة المتبعة.
هل ينطبق ذلك على مجالات أخرى من الحياة، أو على الحياة عمومًا؟ أظن
نعم: إن من يدفع الحياة، من يقف وراء التطور، من يصنع التاريخ، هم
الأشخاص الذين يخرجون عن اتباع الطرق المعبدة ويخرجون عن المألوف.
يعني هذا على صعيد المناهج المدرسيَّة وعلى صعيد "ما هي المدرسة" أنَّ
علينا أنْ نكسر المفاهيم الكبيرة والأساسية الموروثة وأن نبدأ طريقًا
جديدًا!
ولقد يعني ذلك، على صعيد الحروب المدمِّرة التي تحدث في أرجاء مختلفة
من العالم، أنَّ الجميع مسؤول وبنفس الدرجة، وقد يعني أيضًا أن كلَّ
شخص يملك بطريقة ما فرصة ما لصنع المعجزة وتغيير المسار!
*** *** ***
[5]
يمكن أيضًا رؤية محاكاة لنفس الفكرة على الرابط التالي: